Gram-Schmidt

Reminder definitions

Orthogonal- oft interchangeable with perpendicularity at points of intersection.But within linear algebra it is better described as the dot product of two (nonzero) vectors producing a sum of zero.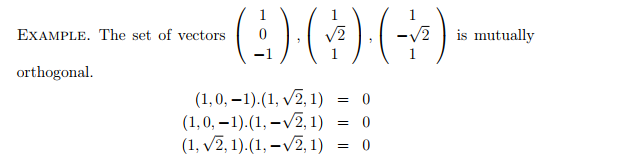  

If the sum of these vectors was anything other than zero, orthogonality is not present

Orthonormal- when orthogonal vectors have a magnitude of 1, both of these conditions need to be met to be considered orthonormal.

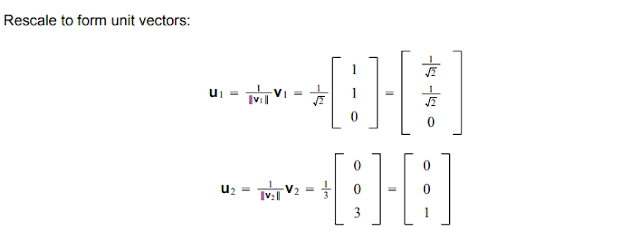Note how the summation of either vector entries will equal total; hence being normalized.
Note: ||v||=(v*v)^(1/2)

Basis- a linearly independent spanning set of vectors within a subspace. Going along with the subject theme, we are concerned with orthonormal basis'.

Gram-Schmidt

• The Gram-Schmidt process allows for linearly independent basis' and orthogonalizes along orthonormalizes the basis.
• 
  
 

• The Gram-Schmidt process can also be used for polynomial basis'; the process is modified slightly in order to account for the basis being able to be orthogonalized easily but not orthonormalized as easily.
• ". For more abstract spaces, however, the existence of an orthonormal basis is not obvious. The Gram-Schmidt algorithm is powerful in that it not only guarantees the existence of an orthonormal basis for any inner product space, but actually gives the construction of such a basis."
• If you are a perpetual cynic like myself, you are probably questioning the importance of  seemingly simple method. 
1. An orthonormal basis is identical to the standard basis and is able to be. 
1. This simplifies problem sets significantly and allows problems to be solved in fewer steps (Thank you zeroes!)
2. This process allows for QR factorization to be completed since Q is composed of an orthogonal matrix and R is composed from a triangular matrix.
1. The determinant is quickly solved & eigenvalues.
2. QR factorization solves complex linear equations and requires matrices(of various sizes) to be easily invertible.
3. Useful in physics; quantum mechanics, and dynamic problems.

Examples

QR factorization

Practice

References

1. Gram-Schmidt (n.d.). [PDF] Available  at:   http://www.math.ucla.edu/~yanovsky/Teaching/Math151B/handouts/GramSchmidt.pdf [Accessed 8 Dec. 2017].    
2. Gram-Schmidt tutorial (n.d.). [PDF] Available at:  https://www.math.hmc.edu/calculus/tutorials/gramschmidt/gramschmidt.pdf  [Accessed 7 Dec. 2017]  
3. Lecture (n.d.). [PDF] Available at:  http://www.math.usm.edu/lambers/mat415/lecture3.pdf [Accessed 8 Dec. 2017].
4. Lesson Plan (n.d.). [PDF] Available at:http://www.ucl.ac.uk/~ucahmdl/LessonPlans/Lesson10.pdf [Accessed 8 Dec. 2017].  
5. Practice. (n.d.). [PDF] Available at: http://www.math.ucsd.edu/~jmckerna/Teaching/14-15/Autumn/20F/practicef.pdf [Accessed 7 Dec. 2017].