Reminder definitions
Orthogonal- oft interchangeable with perpendicularity at points of intersection.But within linear algebra it is better described as the dot product of two (nonzero) vectors producing a sum of zero.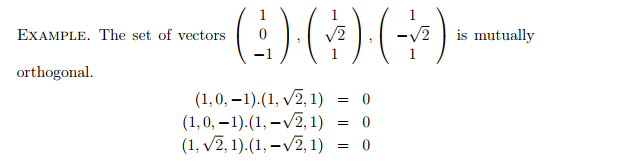 |
| If the sum of these vectors was anything other than zero, orthogonality is not present |
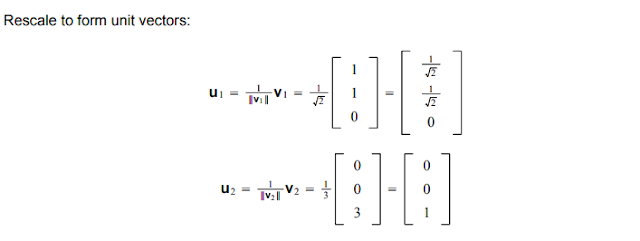 |
| Note how the summation of either vector entries will equal total; hence being normalized. Note: ||v||=(v*v)^(1/2) |
Basis- a linearly independent spanning set of vectors within a subspace. Going along with the subject theme, we are concerned with orthonormal basis'.
Gram-Schmidt
- The Gram-Schmidt process allows for linearly independent basis' and orthogonalizes along orthonormalizes the basis.
- The Gram-Schmidt process can also be used for polynomial basis'; the process is modified slightly in order to account for the basis being able to be orthogonalized easily but not orthonormalized as easily.
- ". For more abstract spaces, however, the existence of an orthonormal basis is not obvious. The Gram-Schmidt algorithm is powerful in that it not only guarantees the existence of an orthonormal basis for any inner product space, but actually gives the construction of such a basis."
- If you are a perpetual cynic like myself, you are probably questioning the importance of seemingly simple method.
- An orthonormal basis is identical to the standard basis and is able to be.
- This simplifies problem sets significantly and allows problems to be solved in fewer steps (Thank you zeroes!)
- This process allows for QR factorization to be completed since Q is composed of an orthogonal matrix and R is composed from a triangular matrix.
- The determinant is quickly solved & eigenvalues.
- QR factorization solves complex linear equations and requires matrices(of various sizes) to be easily invertible.
- Useful in physics; quantum mechanics, and dynamic problems.
Examples
 |
| QR factorization |
Practice
References
- Gram-Schmidt (n.d.). [PDF] Available at: http://www.math.ucla.edu/~yanovsky/Teaching/Math151B/handouts/GramSchmidt.pdf [Accessed 8 Dec. 2017].
- Gram-Schmidt tutorial (n.d.). [PDF] Available at: https://www.math.hmc.edu/calculus/tutorials/gramschmidt/gramschmidt.pdf [Accessed 7 Dec. 2017]
- Lecture (n.d.). [PDF] Available at: http://www.math.usm.edu/lambers/mat415/lecture3.pdf [Accessed 8 Dec. 2017].
- Lesson Plan (n.d.). [PDF] Available at:http://www.ucl.ac.uk/~ucahmdl/LessonPlans/Lesson10.pdf [Accessed 8 Dec. 2017].
- Practice. (n.d.). [PDF] Available at: http://www.math.ucsd.edu/~jmckerna/Teaching/14-15/Autumn/20F/practicef.pdf [Accessed 7 Dec. 2017].

